VARIABLE COMPLEJA.

x,y / x,y
Se definen en este conjunto dos operaciones que lo convierten en una
estructura algebraica.
La suma: Sean z
1
,z
2
; z
1
x
1
,y
1
; z
2
x
2
,y
2

z
1
z
2
x
1
x
2
,y
1
y
2

Propiedades: z
1
,z
2
,z
3
se tiene
1) Asociatividad z
1
z
2
z
3
z
1
z
2
z
3
2) Conmutatividad z
1
z
2
z
2
z
1
3) Existencia de neutro 0 0,0 , z
1
0 0 z
1
z
1
4) Existencia de opuestos z , z tal que z z 0
La multiplicacin: Sean z
1
,z
2
; z
1
x
1
,y
1
; z
2
x
2
,y
2

z
1
z
2
x
1
x
2
y
1
y
2
,x
1
y
2
y
1
x
2

Propiedades: z
1
,z
2
,z
3
se tiene
1) Asociatividad z
1
z
2
z
3
z
1
z
2
z
3
2) Conmutatividad z
1
z
2
z
2
z
1
3) Existencia de neutro 1 1,0 , z
1
1 1z
1
z
1
4) Existencia de inversos z , z 0 z
1
tal que z z
1
1
si z a,b ; z 0 ; z
1
x,y
se tiene a,bx,y 1,0 ax by ; bx ay
ax by 1
bx ay 0
de aqu x
a
a
2
b
2
; x
b
a
2
b
2
z
1

a
a
2
b
2
,
b
a
2
b
2

Obs)
esto haciendo la identificacin siguiente x con x,0 .
ponemos i , i 0,1
se tiene i
2
0,10,1 1,0 de ahi i
2
1
z a,b a,01,0 b,00,1
con la identificacin z a bi (forma a bi de un nmero complejo)
Para z ; z a bi
ponemos a Rez parte real de z y b Imz parte imaginaria de z
Def) Sea z ; z a bi definimos el conjugado de z como
z a bi o sea se le cambia signo a la parte imaginaria.
Propiedades:
1) z
1
z
2
z
1
z
2
2) z
1
z
2
z
1
z
2
3) z z
4) z
1
z
1
5)
z
1
z
2

z
1
z
2
6) z z
0

De la numero 6) se tiene z z a bia bi a

2
b
2
Def) El modulo o valor absoluto del numero complejo z
z z z Rez
2
Imz
2
Propiedades:
1 z 0 z 0 z 0
2) z
1
z
2
z
1
z
2
3) z z
4) z
1
z
1
5)
z
1
z
2

z
1
z
2
6) z
1
z
2
z
1
z
2
7) z
1
z
2
z
1
z
2
Def) Sean z
1
,z
2
la distancia entre estos dos numeros es
d z
1
,z
2
z
1
z
2
z z
0
r es la ecuacin de la circunferencia centrada en z
0
y radio r.
Forma polar de un nmero complejo.
La forma a bi de un numero complejo es la forma cartesiana del punto
a,b
2
.Como es posible representar el mismo punto usando coordenadas
polares se tiene de all la forma polar de un numero complejo.
z a bi , 0 el angulo formado por el lado positivo del eje x la linea que
une el punto z a bi con el origen. Con z que resulta ser la distancia
entre el punto z a bi y el origen.
a z cos0 ; b z sin0
z a bi z cos0 i z sin0 z cos0 i sin0
poniendo z r y con la famosa formula de Euler e
i0
cos0 i sin0
z r e
i0
la forma polar del numero complejo z.
Para un numero complejo el modulo est univocamente determinado,en cambio
el angulo asociado est determinado salvo multiplos de 2m.
El argumento de z ,
argz 0 / z r e
i0
conjunto de los angulos asociados.
se distingue entre ellos el argumento principal.
Para z z 0 Argz es el nico numero real 0 tal que satisface
z r e
i0
y m 0 m.
Multiplicacin.
z
1
r
1
e
io
; z
2
r
2
e
i[
z
1
z
2
r
1
coso i sino r
2
cos[ i sin[
z
1
z
2
r
1
r
2
cosocos[ i sinocos[ i cososin[ sinosin[
z
1
z
2
r
1
r
2
cosocos[ sinosin[ isinocos[ cososin[
z
1
z
2
r
1
r
2
coso [ i sino [
z
1
z
2
r
1
r
2
e
io[
Para z 0 ; z r e
i0
, z
1
r
1
e
i0
Divisin
z
1
z
2

r
1
r
2
e
io[
Potencias z r e
i0
; z
n
r
n
e
in0
n Formula de De Moivre.
z
n
z
1

n
Ejercicios. Calcular.
8 i 8 3
2 3 2i
;
3
2
i
3
2
3
1
6
i
1
6
3

6 3 6i
6 6i

3
, 1 i
23
RAICES.
Sea z ,
n
z w / w
n
z
Aqui w
n
z es un polinomio de grado n en la variable w.
Recuerdo. Teorema fundamental del Algebra.
Todo polinomio de grado mayor que cero tiene al
menos una raiz en el cuerpo de los numeros complejos.
Esto trae como consecuencia de que un polinomio de grado n
tiene exactamente n raices en . Por lo que entonces un numero
complejo distinto de cero tiene exactamente n raices n-esimas en .
Dado z , z r e
i0
y w x e
iy
w
n
z x
n
e
iny
r e
i0
x
n
r de aqui x
n
r ( nica raiz n-esima real )
e
iny
e
i0
se tiene ny 0 2km ; k .
n
z
n
r e
02km
n
i
/ k 0,1,2,3,...,n 1
Ejemplos)
3
1 i
1 i 2 e
m
4
i
;
3
1 i
6
2 e
m
4
2km
3
i
/ k 0,1,2
6
2 e
m
12
i
;
6
2 e
7m
12
i
;
6
2 e
15m
12
i
8
1 ; 1 e
0i
;
8
1 e
2km
8
i
/ k 0,1,2,3,4,5,6,7
1 e
m
4
i
e
m
2
i
e
3m
4
i
e
mi
e
5m
4
i
e
3m
2
i
e
7m
4
i
1
2i 2
2
i
2i 2
2
1
2i 2
2
i
2i 2
2
CONJUNTOS EN EL PLANO COMPLEJO.
Sea z
0
, r , r 0.
Vecindad abierta con centro en z
0
y radio r
Bz
0
,r z / z z
0
r
Vecindad cerrada con centro en z
0
y radio r
Bz
0
,r z / z z
0
r
Vecindad abierta perforada con centro en z
0
y radio r
B

z
0
,r z / 0 z z
0
r
Def) Sea S , z
0
es un punto interior de S si existe
r 0 tal que Bz
0
,r S.
El conjunto de los puntos interiores se llama el interior
de S se anota intS.
El interior del S
c
se llama el exterior de S.
z
0
es un punto frontera de S si toda vecindad de z
0
contiene
puntos de S y de S
c
.El conjunto de los puntos frontera se llama
la frontera de S.
Def) z
0
, S z
0
es un punto de acumulacin de S
si toda vecindad de z
0
contiene al menos un punto de S
distinto de z
0
.O sea r ,r 0 se tiene B

z
0
,r S .
Ejemplo.
S z / z 1
intS S
extS z / z 1
FrS z / z 1
z / z 1 conjunto de puntos de acumulacin de S.
Un conjunto U es abierto si todos sus puntos son interiores,
es decir z U , r 0 tal que Bz,r U.
Un conjunto C es cerrado si C
c
es abierto.
Un conjunto S es un conjunto acotado si existe r 0 tal que
S B0,r.O sea existe M 0 tal que z S , z M.
si no se cumple esto el conjunto es no acotado.
Ejemplo. S z / z 1 es acotado.
U z / z 1 es no acotado.
Un conjunto U es conexo si no puede ser representado por la unin
de dos conjuntos abiertos disjuntos no vacios.Todo par de puntos de U
puede ser unido por una linea poligonal totalmente contenida en U.
Una regin es un conjunto abierto y conexo.
Una regin es simplemente conexa si toda curva cerrada situada en ella
todo el interior de esa curva est en la regin.O sea no tiene agujeros.
Ejercicios.
Clasificar los conjuntos segn los conceptos ya descritos.
1) z / Imz 1
2) z / z 3 4
3) z / 0 argz
m
4
; z 0
LA ESFERA DE RIEMANN.
Consideremos la esfera unitaria S
0
: x
2
y
2
z
2
1
cortada por el ecuador por el plano z 0.Desde el polo
norte N 0,0,1 se traza una linea hacia el plano complejo
que corta a la esfera lo cual produce una aplicacin conocida
como la proyeccin estereogrfica.
: S
0
, a bi
2a
a
2
b
2
1
,
2b
a
2
b
2
1
, 1
2
a
2
b
2
1

A todo punto a bi le corresponde un punto de la esfera.A todo punto
de la esfera,salvo N 0,0,1 le corresponde un nmero complejo.
es un punto ideal al cual le hubiera correspondido el polo norte con
la proyeccin estereogrfica.
Se define el plano complejo extendido.
Con las reglas z z
z z
z

0 ; z
z
0
; z 0
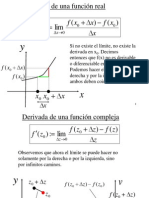
DIFERENCIACIN DE FUNCIONES DE VARIABLE COMPLEJA.
Sea f : S ; S
f es derivable en z
0
si existe el limite lim
zz
0
fz fz
0

z z
0
en el caso de existir se anota f

z
0
.
Obs)
En el caso f : S ; S
f es derivable en z
0
S entonces f

z
0
0.
f

z
0
lim
zz
0
fz fz
0

z z
0
este limite calculado por una recta paralela al eje real resulta
un numero real(complejo sin parte imaginaria).Calculado a
travs de una recta paralela al eje imaginario resulta un numero
imaginario puro(complejo sin parte real).Por lo tanto debe ser cero.
En el caso
f : I con I intervalo real.
ft ut ivt
se tiene que si f es derivable en t
0
I
f

t
0
lim
tt
0
ft ft
0

t t
0
lim
tt
0
ut ivt ut
0
ivt
0

t t
0
f

t
0
lim
tt
0
ut ut
0

t t
0
i
vt vt
0

t t
0
de aqui
f

t
0
u

t
0
i v

t
0

Una curva parametrizada en es el grfico de una funcin

continua , . I con ,t ut i vt
Caso general si f : S ; S
en los puntos donde el limite lim
zz
0
fz fz
0

z z
0
queda definida
una funcin que se llama la derivada de f.
Resultados similares al caso real.
1) f es derivable en z
0
entonces f es continua en z
0
.
porque
fz
fz fz
0

z z
0
z z
0
fz
0

con eso lim

zz
0
fz f

z
0
0 fz
0

lim
zz
0
fz fz
0

entonces f es continua en z
0
.
Reglas de derivacin.
f g

f

g

f
g

f

g fg

g
2
; g 0
z f

z f

f g

f g

f

g g f

z
0
g

fz
0

f

z
0

Por ejemplo.
f g

z
0
lim
zz
0
f gz f gz
0

z z
0
lim
zz
0
f z gz f z
0
gz
0

z z
0
f g

z
0
lim
zz
0
f z gz f z
0
gz f z
0
gz f z
0
gz
0

z z
0
f g

z
0
lim
zz
0
f z f z
0

z z
0
gz
g z gz
0

z z
0
f z
0

f g

z
0
f

z
0
gz
0
g

z
0
f z
0

La derivada direccional.
Sea u , u 0
La recta que pasa por el punto z
0
en la direccin de u son los
puntos del plano tales que z z
0
t u , t .
L z / z z
0
t u , t
L es la curva , : tal que ,t z
0
t u
DEF) La derivada direccional de f en z
0
en la direccin de u
es
f
u
z
0
lim
t0
fz
0
t u fz
0

t
t
Casos especiales
u 1 direccin por el eje real.
f
1
z
0
lim
t0
fz
0
t fz
0

t

f
x
z
0

u i direccin por el eje imaginario .

f
i
z
0
lim
t0
fz
0
t i fz
0

t

f
y
z
0

Las derivadas parciales son casos especiales de derivada direccional.

Teorema:
Si f es derivable en z
0
entonces existen all las derivadas
parciales y se tiene que
f
x
z
0
i
f
y
z
0
0
Dem)
f

z
0
lim
zz
0
fz fz
0

z z
0
calculado este limite siguiendo la trayectoria de la recta z z
0
t
se tiene f

z
0
lim
t0
fz
0
t fz
0

t

f
x
z
0

calculado este limite siguiendo la trayectoria de la recta z z

0
t i
se tiene f

z
0
lim
t0
fz
0
t i fz
0

t i
i
f
y
z
0

restando se obtiene
f
x
z
0
i
f
y
z
0
0
Con z x iy y fz ux,y ivx,y

u
x
z
0
i
v
x
z
0
i
u
y
z
0
i
v
y
z
0
0
de all

u
x
z
0

v
y
z
0
i
u
y
z
0

v
x
z
0
0
con lo que se tiene en z
0
u
x

v
y
u
y

v
x
ECUACIONES DE CAUCHY-RIEMANN.
Luego el teorema puede enunciarse tambin
f derivable en z
0
se cumplen en z
0
u
x

v
y
u
y

v
x
ECR.
La contrapositiva nos dice
En algn z
0
alguna de las ecuaciones
u
x

v
y
u
y

v
x
no se cumple
entonces f no es derivable all.
Ejemplo:
fz z x iy ux,y ivx,y
ux,y x vx,y y
u
x
1 ; z x iy
v
y
1 ; z x iy
u
x

v
y
; z
luego fz z no es derivable en ningn z .
Entonces las ecuaciones de Cauchy-Riemann son una condicin
necesaria para que una funcin compleja sea derivable.
Sin embargo no son suficientes para la derivabilidad de una funcin
compleja porque que se cumplan las ecuaciones de Cauchy-Riemann
en un punto no garantizan que la funcin sea derivable all.
Ejemplo.
La funcin fz u iv
con ux,y
x
3
y
3
x
2
y
2
si x,y 0.0
0 si x,y 0.0
vx,y
x
3
y
3
x
2
y
2
si x,y 0.0
0 si x,y 0.0
u
x
0,0 lim
h0
uh,0 u0,0
h
1 ;
u
y
0,0 lim
h0
u0,h u0,0
h
1
v
x
0,0 lim
h0
vh,0 v0,0
h
1 ;
v
y
0,0 lim
h0
v0,h v0,0
h
1
u
x
0,0
v
y
0,0
u
y
0,0
v
x
0,0
se cumplen las ecuaciones de Cauchy-Riemann en z 0.
f

0 lim
z0
fz f0
z 0
lim
z0
fz
z

x
3
y
3
x
2
y
2
i
x
3
y
3
x
2
y
2
x iy
Calculado el limite por la recta z 0 t 1 t
se tiene
lim
t0
fz
z
lim
t0
t
3
0
t
2
0
i
t
3
0
t
2
0
t
lim
t0
t i t
t
1 i
Calculado el limite por la recta z t t i
se tiene
lim
t0
fz
z
lim
t0
0 i
2t
3
2t
2
t i t
lim
t0
t i
t i t

i
1 i

1
2

1
2
i
como estos limites no coinciden el limite lim
z0
fz f0
z 0
no existe por lo que f no es derivable en z 0.
Condiciones para la suficiencia.
Sean u : S v : S con S
un conjunto abierto de
2
.Supongamos que las cuatro
funciones
u
x
,
v
x
,
u
y
,
v
y
son continuas en S.
Si en algn punto z
0
S se cumplen
u
x

v
y
u
y

v
x
las ECR.Entonces fz u iv es derivable en z
0
.
Ejemplo: fz e
x
2
y
2
cos2xy i e
x
2
y
2
sin2xy
u
x
2e
x
2
y
2
xcos2xy ysin2xy
v
y
u
y
2e
x
2
y
2
ycos2xy xsin2xy
v
x
Las ecuaciones de Cauchy-Riemann se cumplen en
todos los puntos de . Adems las funciones
u
x
,
u
y
,
v
x
,
v
y
son todas continuas en .
Por lo que f es derivable en todo .
Def) Sea f u iv funcin de variable compleja.
f es analitica en z
0
si existe una vecindad
de z
0
; B z
0
,r tal que f es derivable en todos
los puntos de esa vecindad.
f derivable en z , z B z
0
,r
f es analitica en un conjunto abierto S
si es analitica en cada punto de S.
Obs) Una funcin puede ser derivable en un punto y
no ser analitica all.
Ejemplo: fz |z|
2
z x iy ; fz u iv x
2
y
2
0i
u
x
2x
v
y
0 se cumple para x 0
u
y
2y
v
x
0 se cumple para y 0
Esto nos dice que en el nico punto que se cumplen
las ECR es en z 0.La funcin no tiene derivada para
z 0.
Veamos f

0 lim
z0
|z|
2
0
z 0
lim
z0
z z
z
0
Entonces f es derivable en z 0 pero no es analitica all.
Una funcin compleja se llama entera si es analitica en todo .
Ejemplo los polinomios son funciones enteras.
Sea f analitica en z
0
, f u iv y supongamos que
u y v tienen segundas derivadas parciales continuas
entonces de
u
x

v
y
se obtiene

2
u
x
2


2
v
yx
de
u
y

v
x
se obtiene

2
u
y
2


2
v
xy
al sumar se tiene

2
u
x
2


2
u
y
2
0
analogamente resulta

2
v
x
2


2
v
y
2
0
La ecuacin diferencial

2
u
x
2


2
u
y
2
0
se conoce como la ecuacin de Laplace.
Una funcin ux,y con segundas derivadas parciales
continuas que satisface la ecuacin de Laplace en una
regin del plano complejo se llama armonica en .
Teorema:
fz ux,y i vx,y analitica en una regin
entonces ux,y ,vx,y son armonicas
en .
Def) vx,y es armonica conjugada de ux,y si son
ambas armonicas y satisfacen las ecuaciones de
Cauchy-Riemann.
Obs) Dada una funcin armonica siempre existe "su"
conjugada.
Ejemplo:
ux,y y
3
3x
2
y es armonica.
u
x

v
y
6xy
v
y
6xy de donde vx,y 3xy
2
cx
u
y

v
x
implica 3y
2
3x
2
3y
2
c

x
c

x 3x
2
de donde cx x
3
C
vx,y x
3
3xy
2
por lo que fz y
3
3x
2
y i x
3
3xy
2

es analitica
Notar que f

z
f
x
6xy i3x
2
3y
2

FUNCIONES ELEMENTALES.
1) Polinomios.
fz pz a
0
a
1
z a
2
z
2
...a
n
z
n
; a
i
.
p : es una funcin entera.
analitica en todo y por lo tanto derivable y continua.
z
0
es una raiz (cero) de multiplicidad k , k , de pz
si y solo si pz z z
0

k
qz ; qz
0
0.
2) Funciones racionales.
Rz
pz
qz

a
0
a
1
z a
2
z
2
...a
n
z
n
b
0
b
1
z b
2
z
2
...b
m
z
m
;
a
n
0
b
m
0
Rz es analitica en salvo z
1
, z
2
, z
3
,..., z
m
raices de qz.
pz y qz sin factores comunes.
Def)
z
0
es una raiz de multiplidad k de Rz z
0
es una raiz de multiplidad k de pz.
z
0
es una polo de multiplidad k de Rz z
0
es una raiz de multiplidad k de qz.
Obs)
Rz y R

z tienen los mismos polos.

Def)
es una raiz de multiplidad k de Rz 0 es una raiz de multiplidad k de R
1
z
.
es una polo de multiplidad k de Rz 0 es una raiz de multiplidad k de R
1
z
.
Teorema:
Una funcin racional Rz tiene(contando multiplicidades) tantos polos
como ceros en . Este numero adems es el maximo entre los grados
de pz y qz.
Rz
pz
qz

a
0
a
1
z a
2
z
2
...a
n
z
n
b
0
b
1
z b
2
z
2
...b
m
z
m
z
nm
a
0
z
n

a
1
z
n1
.....
a
n
z
0
b
0
z
m

b
1
z
n1
.....
b
m
z
0
R
1
z
z
mn
a
0
z
n
a
1
z
n1
a
2
z
n2
...a
n
b
0
z
m
b
1
z
m1
b
2
z
m2
...b
m
Casos Ceros Polos
n m n m de orden n m
n m n m
n m n de orden m n m
3) La funcin exponencial:
x , e
x
la funcin cumple basicamente que e
x
1
x
2
e
x
1
e
x
2
se trata de extender esta funcin a de modo que cumpla e
z
1
z
2
e
z
1
e
z
2
Def)
Sea z , z x iy e
z
e
x
cosy ie
x
siny
Propiedades.
a) e
z
extiende a e
x
si z x i0 , e
z
e
x
b) z
1
x
1
iy
1
z
2
x
2
iy
2
e
z
1
e
x
1
cosy
1
ie
x
1
siny
1
e
z
2
e
x
2
cosy
2
ie
x
2
siny
2
e
z
1
e
z
2
e
x
1
cosy
1
ie
x
1
siny
1
e
x
2
cosy
2
ie
x
2
siny
2

e
z
1
e
z
2
e
x
1
x
2
cosy
1
cosy
2
siny
1
siny
2
ie
x
1
x
2
siny
1
cosy
2
cosy
1
siny
2

e
z
1
e
z
2
e
x
1
x
2
cosy
1
y
2
ie
x
1
x
2
siny
1
y
2

e
z
1
e
z
2
e
z
1
z
2
c) e
z
e
x
d) y arge
z

e) e
z
e
z
f) z iy se tiene la formula de Euler. e
iy
cosy i siny.
g) e
z
e
x
cosy ie
x
siny ux,y ivx,y
ux,y e
x
cosy vx,y e
x
siny
u y v son armonicas conjugadas
e
z
analitica en .
h)
d
dz
e
z

e
z
x
e
x
cosy ie
x
siny e
z
i) e
z
es peridica de periodo 2mi.
e
z2kmi
e
z
e
2kmi
e
z
j) e
z
0 , z .
Los ultimos dos puntos nos dicen que la funcin exponencial no es
uno a uno(inyectiva) y que el recorrido es 0.
Para conseguir que la funcin quede uno a uno se puede restringir
el dominio () en franjas de la forma x m y 2km m
k 0, 1, 2,......Otra opcin es considerar el recorrido 0
distinto segn e
z
se aplique a las franjas con k 0, 1, 2,.....
Para eso se imagina el recorrido agrandado a infinitas copias 0
apiladas en capas una sobre otra cada una cortada por el eje real negativo
con el borde superior de una capa pegada al borde inferior de la otra.
R conjunto de todas las capas.Cada punto de R est determinado
univocamente en coordenadas polares.
exp : R expz e
z
es uno a uno.
Al conjunto R se le llama superficie de Riemann.
Las lineas de corte en cada copia de 0 cortes de ramificacin.
Los extremos de los cortes 0 y puntods de ramificacin.
Cada copia de 0 una rama de R.
4) Las funciones trigonometricas.
De la formula de Euler e
i0
cos0 i sin0 , 0
se tiene e
i0
cos0 i sin0 de all
cos0
e
i0
e
i0
2
sin0
e
i0
e
i0
2
Def)
z ; cosz
e
iz
e
iz
2
sinz
e
iz
e
iz
2i
claramente extienden a las funciones reales y claramente son
enteras.
d
dz
cosz sinz
d
dz
sinz cosz
Las otras definiciones y sus derivadas.
tanz
sinz
cosz
d
dz
tanz sec
2
z
cotz
cosz
sinz
d
dz
cotz csc
2
z
secz
1
cosz
d
dz
secz secz tanz
cscz
1
sinz
d
dz
cscz cscz cotz
Identidades bsicas.
cos
2
z sin
2
z
e
iz
e
iz
2

2

e
iz
e
iz
2i

2
cos
2
z sin
2
z
e
2iz
e
2iz
2
4

e
2iz
e
2iz
2
4

cos
2
z sin
2
z 1
sin2z
e
2iz
e
2iz
2i
2
e
iz
e
iz
2i
e
iz
e
iz
2
sin2z 2sinz cosz
sinz w
e
izw
e
izw
2i

e
iz
e
iw
e
iz
e
iw
2i
sinz cosw
e
iz
e
iz
2i
e
iw
e
iw
2

e
iz
e
iw
e
iz
e
iw
e
iz
e
iw
e
iz
e
iw
4i
cosz sinw
e
iz
e
iz
2
e
iw
e
iw
2i

e
iz
e
iw
e
iz
e
iw
e
iz
e
iw
e
iz
e
iw
4i
sinz w sinz cosw cosz sinw
Para la forma fz u iv
cosz cosx iy
e
ixy
e
ixy
2
cosz
e
y
cosx i sinx e
y
cosx i sinx
2
cosz cosx
e
y
e
y
2
i sinx
e
y
e
y
2
cosz cosx coshy i sinx sinhy
5) Las funciones hiperbolicas.
Def) coshz
e
z
e
z
2
sinhz
e
z
e
z
2
claramente extienden a las funciones hiperbolicas reales y
tambin son enteras.
d
dz
coshz sinhz
d
dz
sinhz coshz
Las otras definiciones y sus derivadas.
tanhz
sinhz
coshz
d
dz
tanhz
cothz
coshz
sinhz
d
dz
cothz
sechz
1
coshz
d
dz
sechz
cschz
1
sinhz
d
dz
cschz
Identidades bsicas.
cosh
2
z sinh
2
z
e
z
e
z
2

2

e
z
e
z
2

2
cosh
2
z sinh
2
z 1
sinhiz
e
iz
e
iz
2
i sinz ; coshiz
e
iz
e
iz
2
cosz
6) El logaritmo.
z
logz w / e
w
z
log0
En adelante z 0 con lo que z 0
w u iv logz entonces e
uiv
z
e
u
cosv ie
u
sinv z de aqui v argz
z e
u
cosv
2
e
u
sinv
2
e
u
de aqui u ln z es decir todos con la misma parte real.
logz ln z i argz w ln z iv / v argz
Ahora sea fz una funcin continua definida en una rama de logz,
fz logz entonces f es analitica.
fz fz
0

z z
0

fz fz
0

e
fz
e
fz
0

e
fz
e
fz
0

fz fz
0

1
z z
0

e
fz
0

1

1
z
0
d
dz
logz
1
z
A la rama de R cortada a lo largo del eje real negativo que se mapea
en la franja m y m se le llama la rama principal del logaritmo.
log es el logaritmo principal.
Ejemplos
log1 0 im 2km , k .
el principal log1 mi
Si x , x 0 z x 0i
logz ln|z| i argz el principal
logz lnx extiende al logaritmo real.
7) Potencias.
Sea z , z 0 , w
z
w
e
wlogz
es analitica porque es compuesta de funciones analiticas.
El valor principal est dado por el logaritmo principal.
d
dz
z
w

d
dz
e
wlogz
e
wlogz

w
z
w z
w1
Ejemplo
i
i
e
i logi
e
i
m
2
i2kmi
e
m
2
2km
potencia principal
i
i
e
m
2
8) Funciones trigonometricas inversas.
Def)
arccosz w / cosw z
arcsinz w / sinw z
arctanz w / tanw z
Por ejemplo
w arctanz se tiene que tanw z
e
iw
e
iw
2i
e
iw
e
iw
2
z
e
iw
e
iw
e
iw
e
iw
i z

e
2iw
1
e
2iw
1
i z e
2iw
1 i z e
2iw
i z
e
2iw
1 i z 1 i z e
2iw

1 i z
1 i z
2i w log
1 i z
1 i z
w
1
2i
log
1 i z
1 i z
por lo que arctanz
1
2i
log
1 i z
1 i z

i
2
log
i z
i z
arctanz
i
2
log
i z
i z
; z i
d
dz
arctanz
d
dz

i
2
log
i z
i z

i
2
i z
i z
i z i z
i z
2
d
dz
arctanz
i
2
i z
i z
2i
i z
2

1
1 z
2
d
dz
arctanz
1
1 z
2