Arkansas Tech University

MATH 2914: Calculus I

Dr. Marcel B. Finan
37 Finding Antiderivatives Graphically and
Numerically
Recall that if a function f(x) is given then the new function f

(x) is called
the derivative of f(x). For example, if f(x) = x
2
then f

(x) = 2x. This

process is referred to as dierentiation.
Now, if instead f

(x) is known then the process of nding f(x) is called inte-

gration or antidierentiation. In this case, we call f(x) an antideriva-
tive of f

(x). In general, if f and F are two functions such that F

= f
then we say that F(x) is an antiderivative of f(x). For example, x
2
is an
antiderivative of 2x since (x
2
)

= 2x. Note that, there are innitely many

antiderivatives of 2x, namely, x
2
+ C where C is a constant. We call x
2
+ C
the general antiderivative ( or the indenite integral) of x
2
and we
represent this symbolically by

2xdx = x
2
+ C.
Next, we see how to reconstruct the graph of f given the graph of its deriva-
tive f

.
Example 37.1
The graph of f

(x) is given in Figure 37.1.

Figure 37.1
1
Sketch a graph of the function f(x) satisfying f(0) = 1.
Solution.
Note that f

(x) is always increasing so that f

(x) > 0 and therefore the

graph of f(x) is always concave up. Since f

(x) < 0 for x < 0, f(x) is de-

creasing there. Similarly, since f

(x) > 0 for x > 0, f(x) is increasing there.

Since f

(0) = 0 and f(x) is decreasing and then increasing, we conclude that

x = 0 is a minimum. A graph of f(x) is given in Figure 37.2.
Figure 37.2
Example 37.2
The graph of f

(x) = e
x
2
is given in Figure 37.3.
Figure 37.3
Sketch the graph of f(x) satisfying f(0) = 0.
Solution.
f

(x) is always positive implies the graph of f(x) is always increasing. Now,
for x < 0, f

(x) is increasing so that f

(x) > 0 and therefore f(x) is concave

2
up. For x > 0 the function f

(x) is decreasing and so f

(x) < 0. That is,

f(x) is concave down there. Thus, x = 0 is a point of inection. Finally,
since lim
x
f

(x) = 0, the graph of f(x) levels o at both ends. See Figure

37.4.
Figure 37.4
Next, we will reconstruct numerically the antiderivative f by using the Fun-
damental Theorem of Calculus: If F

(x) = f(x) then

b
a
f(x)dx = F(b)
F(a). In particular, we have

b
a
f

(x)dx = f(b) f(a).

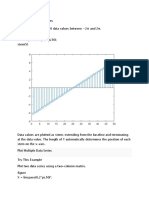
Example 37.3
Given the values of f

(x) in the table and that f(0) = 100 estimate f(x) for
x = 2, 4, 6.
x 0 2 4 6
f

(x) 10 18 23 25
Solution.
Applying the Fundamental Theorem of Calculus on the interval [0, 2] we nd
f(2) f(0) =

2
0
f

(x)dx.
Thus,
f(2) = f(0) +

2
0
f

(x)dx.
3
To estimate the integral we nd the left-hand sum and the right-hand sum
and take the average of that. The left-hand sum is f

(0)(2) = 20 and the

right-hand sum is f

(2)(2) = 36. Thus,

2
0
f

(x)dx =
20 + 36
2
= 28
and so
f(2) = 100 + 28 = 128.
Similarly, we have
f(4) = f(2) +

4
2
f

(x)dx
with

4
2
f

(x)dx =
36 + 46
2
= 41
so that
f(4) = 128 + 41 = 169.
Finally, we have
f(6) = f(4) +

6
4
f

(x)dx = 169 + 48 = 217

Now, recall that for f(x) 0 the denite integral

b
a
f(x)dx represents the
area under the graph of f(x) between the lines x = a and x = b. If the region
is below the x-axis then

b
a
f(x)dx is the negative of the area of that region.
Example 37.4
Figure 37.5 shows the graph of f

(x). Suppose that f(1) = 2. Find

f(0), f(1), and f(3).
Figure 37.5
4
Solution.
By the FTC we have
f(b) = f(1) +

b
1
f

(x)dx.
Thus,
f(0) =f(1) +

0
1
f

(x)dx
=2 +
1
2
(1 2) = 1
f(1) =f(0) +

1
0
f

(x)dx
=1 + 1 2 = 1
f(3) =f(1) +

3
1
f

(x)dx = 1 +
1
2
(2 2) = 3
where we compute

t
a
f

(x)dx by determining the area between f

and the
horizontal axis for a x t.
5